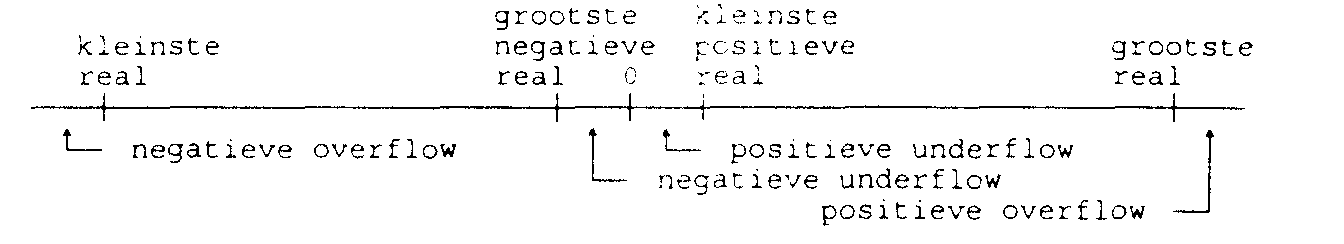
Excess 2 n-1
Het getal n in deze uitdrukking staat voor liet aantal gebruikte bits om getallen te bewaren . In deze serie voorbeelden met 8 bits-getallen geldt dus n - 1 = 7, ofwel excess-128. Het recept luidt: bij elk getal (positief, nul of negatief) 128 optellen en daarvan het binaire equivalent maken.
+128
+128
Merk nog op dat voor niet-negatieve integers de 128 erbij in dit systeem er op neer komt dat, vergeleken met de 'normale' representatie uit de andere systemen, het voorste bit een 1 wordt:
|
53<10> = |
10110101 |
|
|
128<10> = |
10000000 |
|
|
-------- + |
||
|
10110101 |
(53 < 10 > in het excess-128 systeem) |
De grootste integer in dit systeem is dus 11111111 = 127 < 10 > De representatie van het getal nul is 10000000. De kleinste integer wordt weergegeven door 00000000. In de andere systemen stelt dit 0 voor, maar om in dit excess-systeem hier op uit te komen is er 128 teveel bij opgeteld. Met andere woorden: de waarde van de kleinste integer moet wel -128 <10> zijn.
Voor alle duidelijkheid: het excess-systeem werkt op 'alle' getallen, terwijl bij de andere systemen er alleen iets bijzonders gebeurt bij negatieve getallen. In deze drie systemen is de representatie van elke positieve integer dus gelijk.
Opdrachten
Drijvende komma (Floating point) getallen
Het decimale getal 6,5 kan op verschillende manieren worden geschreven: 6,5 = 6,5 * 10 0 = 0,65 * 10 1 = 0,065 * 10 2
De gecursiveerde versie is van de vorm f * 10 x met 0,1 <= f < 1 ofwel 10 -1 <= f <10 -1
Het gedeelte 0,65 kan worden geschreven als 0,65 = 6 * 10 -1 + 5 * 10 -2
Op vergelijkbare wijze gaat men te werk om een decimaal getal als 6,5 binair weer te geven. Het wordt geschreven in de vorm f * 2 x
waarin 2 -1 <= f < 2 0 ofwel 0,5 <= f < 1
en met f = .. * 2 -1 + .. * 2 -2 + ..* 2 -3 + …
Het getal f wordt de fractie (of mantisse) genoemd en het getal x de exponent.
In het volgende voorbeeld worden de benodigde handelingen uitgevoerd. Allereerst wordt door herhaald te vermenigvuldigen met 2 of door herhaald te delen door 2 het getal in de vorm f * 2x geschreven. Dan blijkt te gelden: 6,5 = 0,8125 * 2 3
|
6,5 |
|
|
0,8125 |
|
|
|
:2 |
|
0,5 |
|
|
|
|
|
---------- - |
= 2-1 |
|
3,25 |
|
|
0,3125 |
|
|
|
:2 |
|
0,25 |
|
|
|
|
|
---------- - |
= 2-2 |
|
1,625 |
|
|
0,0625 |
|
|
|
:2 |
|
0,0625 |
|
|
|
|
|
---------- - |
= 2-4 |
|
0,8125 |
|
|
0 |
|
Dan blijkt dat 0,8125 = 1 * 2 -1 + 1 * 2-2 + 1 * 2-4.
Het totaalresultaat kan worden geschreven als:
|
6,5 = |
+ |
23 * |
(1 * 2-1 + 1 * 2-2 + 0 * 2-3 + 1 * 2-4) |
|
0 |
1000011 |
11010000 |
In de weergegeven representatie is een 16 bits floating point systeem gebruikt met:
Door de wijze waarop een real getal wordt weergegeven is er altijd sprake van 1 * 2-1 zodat het meest linkse bit van de fractie altijd 1 is. Dit bit kan dus worden weggelaten en men spreekt dan van een systeem met een hidden bit. Ter illustratie is zijn hieronder de binaire weergaven van 6,5 zonder en mèt hidden bit afgedrukt:
6,5 = 0 1000011 11010000 (zonder hidden bit)
6,5 = 0 1000011 10100000 (met hidden bit)
Het voordeel is een grotere nauwkeurigheid: zonder hidden bit kan in bovenstaand systeem onderscheid worden gemaakt tot en met 2-8 en met een hidden bit zou dat kunnen tot en met 2-9.
In het geschetste systeem zonder hidden bit, heeft de kleinste positieve real die gemaakt kan worden de representatie 0 0000000 10000000 met als decimale waarde 2-65
De wijze waarop reals in elkaar zitten, heeft tevens als consequentie dat 0 als real getal niet 'gemaakt' kan worden.
Opdrachten
Het feit dat voor een floating point systeem ook een eindig aantal bits gereserveerd wordt, heeft consequenties die op de volgende getallenlijn staan afgebeeld:
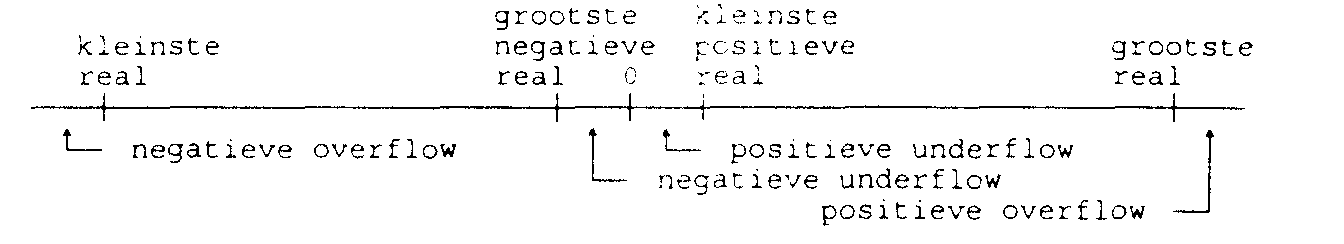
Alle denkbare getallen tussen 0 en de kleinste positieve real kunnen niet worden weergegeven. Men spreekt dan van positieve underflow. Analoog wordt gesproken over negatieve underflow. In de intervallen waar wel getallen kunnen worden weergegeven, zitten nog oneindig veel getallen die alleen maar benaderd kunnen worden en niet exact kunnen worden weergegeven. Als zeer kleinschalig voorbeeld kijken we naar een floating point systeem met 1 tekenbit, een excess 2 systeem voor de exponent en een 2 bits fractie zonder hidden bit.
|
tekenbit |
excess 2 |
|
2 bits fractie |
|
|
0 |
00 |
dwz -2 |
10 |
dwz 1/2 |
|
1 |
01 |
dwz -1 |
11 |
dwz 3/4 |
|
|
10 |
dwz 0 |
|
|
|
|
11 |
dwz 1 |
|
|
In dit systeem zijn acht positieve getallen te maken waarvan de kleinste vier hieronder zijn weergegeven:
0 00 10 = 2 -2 * 1/2 = 1/8
0 00 11 = 2 -2 * 3/4 = 3/16
0 01 10 = 2 -1 * 1/2 = 1/4
0 01 11 = 2 -1 * 3/4 = 3/8
Alle denkbare getallen tussen 3/8 en 3/16 zijn niet te 'maken'.
Het gevolg is dat er met benaderingen gewerkt wordt, hetgeen leidt tot berekeningen waar 'met de hand' wel 0 uitkomt maar met de computer niet. In Turbo Pascal geldt bijvoorbeeld:
( 6 / 7 ) 2 - 4 * ( 9 / 49 ) = 5,42101086242E-20
Gemengde opgaven